1. Phase matching
The physical essence of phase matching is to make the frequency doubled light excited by the fundamental frequency light at each point along the crystal have the same phase when propagating to the emitting surface, so that they can interfere with each other and enhance each other, so as to achieve a good frequency doubling effect.
2. Constraints of phase matching
In order to realize the effective conversion of nonlinear wavelength, it is necessary to meet the conservation of photon energy and photon momentum at the same time in the process of nonlinear optics. Photon momentum conservation ΔK = k3-k1-k2 = 0, which is called the constraint of “phase matching”.
3. Classification of phase matching
There are four classification criteria for phase matching:
(1) The polarization state of illumination light wave can be divided into type I matching and type II matching. If the polarization states of two low-frequency lights are the same, it is type I matching; if the polarization states of two low-frequency lights are orthogonal, it is type II matching;
(2) According to the direction of light wave, phase matching can be divided into collinear and non collinear structures;
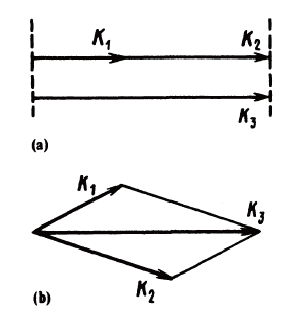
Fig. 1 Collinear or scalar (a) and non collinear or vector (b) three wave interaction phase matching
(3) the phase matching types of nonlinear uniaxial crystals can be divided into six types:
Negative uniaxial crystal (no > ne):
type I(-) ko1+ko2=ke3(θ) — “ooe”
type II(-) ke1(θ)+ko2=ke3(θ) — “eoe”
type II(-) ko1+ke2(θ)=ke3(θ) — “oee”
Positive uniaxial crystal (ne > no):
type I(+) ke1(θ)+ke2(θ)=ko3 — “eeo”
type II(+) ko1(θ)+ke2(θ)=ko3 — “oeo”
type II(+) ke1(θ)+ko2=ko3 — “eoo”
(Note: k-wave propagation vector (k = 2πn/λ); In crystal θ Phase matching angle; o ordinary polarization, e extraordinary polarization; The indexes of 1, 2 and 3 correspond to the wave vector with the longest (1), middle (2) and shortest (3) wavelength)
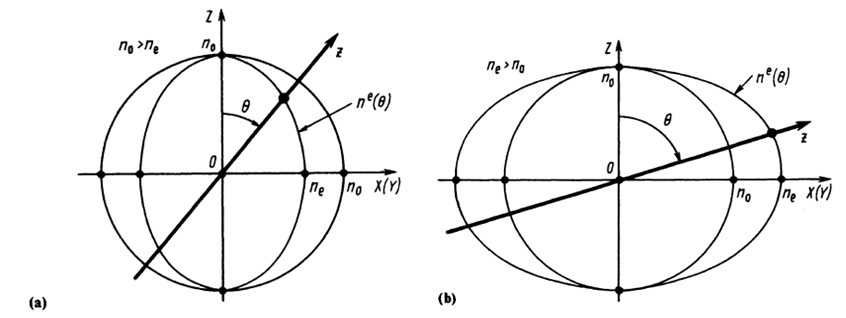
Fig. 2 Relationship between refractive index and light propagation direction and polarization (refractive index plane) in negative (a) and positive (b) uniaxial crystals
(4) In biaxial crystals, only three general types of phase matching occur: ss-f, sf-f and fs-f (the third index corresponds to a higher frequency ω3) ; We mark ss-f case as type I phase matching and sf-f or fs-f case as type II phase matching.
4. Phase matching method
Phase matching methods mainly include birefringence phase matching (BPM) and quasi phase matching (QPM), but BPM method has some deformation methods. Here we mainly talk about critical phase matching and noncritical phase matching. These four methods are briefly introduced below:
BPM is a method to realize the phase matching of nonlinear process by using the birefringence characteristics of nonlinear crystals. For type I phase matching, the signal and idle frequency (or two input waves generating frequency doubling or sum frequency) have the same polarization; For type II phase matching, these waves have orthogonal polarization states.
QPM is a method similar to the phase matching result of nonlinear interaction, especially based on X(2) nonlinear frequency conversion. The uniform nonlinear crystal material is replaced by the material with spatial modulation nonlinearity. The essence of the method is to allow the phase mismatch at some propagation distances, but reverse (or destroy) the nonlinear interaction at some positions, otherwise the interaction will occur in the wrong conversion direction.
Critical phase matching, also known as angle phase matching, is a method of phase matching for some nonlinear processes (usually nonlinear frequency conversion) in birefringent crystals. The interacting beam forms a certain angle with the axis of the refractive index ellipsoid. In almost all cases, one or two waves are linearly polarized along one axis of the refractive index ellipsoid (ordinary beam), while the other or two waves are polarized at a variable angle on the plane across the other two axes (special beam). The adjustment of propagation angle will affect the refractive index of abnormal beam (called abnormal refractive index), while the refractive index of ordinary beam remains unchanged. For some angular positions, phase matching can be realized, that is, the phase mismatch disappears.
Noncritical phase matching, sometimes referred to as temperature phase matching or 90° phase matching, is a method of phase matching for nonlinear processes (usually nonlinear frequency conversion, such as frequency doubling or parametric amplification). The interacting beams are arranged in a row so that they propagate along an axis of the nonlinear birefringent crystal. The phase mismatch is minimized by adjusting the crystal temperature.
5. Phase matching angle
In order to realize the effective conversion of nonlinear wavelength, it is necessary to meet the conservation of photon energy and photon momentum at the same time in the process of nonlinear optics. Photon momentum conservation ΔK = k3-k1-k2 = 0, which is called the constraint of “phase matching”.
6. Coordinate system for calculating uniaxial phase matching angle
The principal axis of uniaxial crystal can be arbitrarily selected perpendicular to the XY plane. For convenience, select the Y-axis direction so that the given wave normal direction is located in the YOZ plane, the Z-axis is the optical axis direction, and K is the propagation vector under the condition of phase matching, so that the fundamental frequency light is o light and the frequency doubled light is e light, θ is the angle between the wave vector K and the Z-axis, ф is the angle between the projection of the wave vector K on the XOY plane and the X-axis.
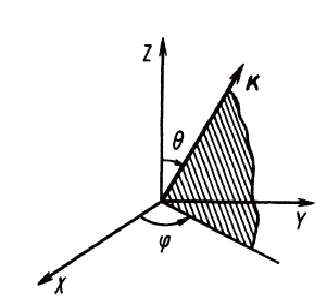
Fig. 3 Unxiaxial crystal coordinate system
7. Calculate uniaxial phase matching angle
The dispersion characteristics of uniaxial nonlinear crystals are determined only by angle θ decision. Therefore, to find the phase matching direction in uniaxial crystal, we only need to determine the corresponding phase matching angle under the three wave interaction θpm. Table 1 shows the exact analytical expression of θpmooe,θpmoeo and θpmeoo, as well as the approximate expression of θpmeoe,θpmoee and θpmeeo, (measurement accuracy: 0.1°-0.2° ).
Phase matching is independent of azimuth ϕ, that is, at the vertex angle 2θpm is realized on the conical surface. At the same time, the efficiency of nonlinear conversion process is determined by θpm and ϕ.
The expression in table 1 can be extended to non collinear phase matching.
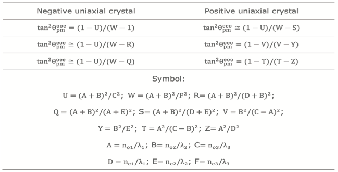
Table. 1 Formula for calculating phase matching angle in uniaxial crystal
8. Phase matching angles of several common crystals
The phase matching angles of some common crystals (Table 2) and class I phase matching angle curve of BBO (Fig. 4) are given here.
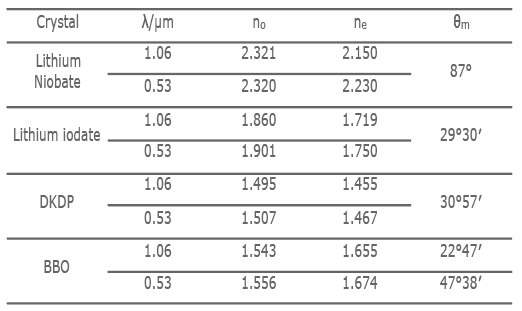
Table. 2 Phase matching angle
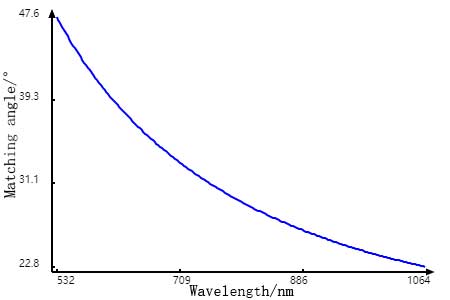
Fig. 4 BBO (o + o → e) phase matching angle curve
9. How to process accurate material phase matching angle?
In the above, we have introduced the concept of phase matching angle. Phase matching angle refers to the angle between the fundamental frequency light in the crystal and the Z direction of the crystal optical axis, rather than the angle with the normal of the incident plane. In order to reduce reflection loss and facilitate adjustment, the fundamental frequency light is generally expected to be incident on the crystal surface in the experiment, as shown in the figure below. Therefore, when processing frequency doubling crystal, the crystal must be cut in a certain direction to make the normal direction of the crystal and the direction of the optical axis θm. It should be noted here that the phase matching angle of the crystal must be selected, for some crystals, its phase matching angle is not unique. Take KDP crystal as an example. KDP crystal is a negative uniaxial crystal, which interacts with class I matched o + o → e and class II matched o + e → e. The phase matching angles corresponding to the two matching methods are θm= 41.2° and θm= 59.1°.
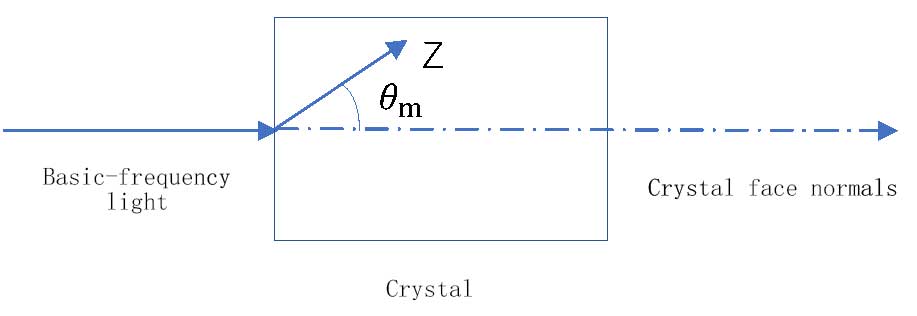
Fig. 5 Cutting of nonlinear crystals
10. How do users match the application requirements and select the appropriate phase matching angle of materials?
As mentioned above, the phase matching angle of some crystals is not unique. In this case, how can we choose the appropriate phase matching angle? We usually choose the appropriate material and phase matching angle according to the tuning range, gain bandwidth, conversion efficiency, effective nonlinear coefficient and other parameters. Briefly cite KDP and BBO to illustrate. As mentioned above, the phase matching angle corresponding to different interactions of KDP is different. Generally, class II matched phase matching angle will be selected in application, because the class I effective nonlinear coefficient dIeff=0.3pm/V (ϕ=45°) of KDP is less than class II effective nonlinear coefficient dIIeff=0.4pm/V (ϕ=0). Class I phase matching of BBO is widely used in optical parametric chirped pulse amplification (OPCPA) because of its wide tuning range, wide gain bandwidth and high conversion efficiency, class II phase matched narrow bandwidth laser can meet the needs of tunable narrow-band laser light source for spectral measurement devices in the fields of chemistry, agriculture, medicine, telecommunications and so on.
Reference
[1] https://www.rp-photonics.com/phase_matching.html
[2] https://www.rp-photonics.com/critical_phase_matching.html
[3] https://www.rp-photonics.com/noncritical_phase_matching.html
[4] https://www.rp-photonics.com/quasi_phase_matching.html
[5] Phase Matching of SHG (wavequanta.com)-BBO、KDP、KBBF、BIBI、LBO phase matching supporting calculator
[6] Dmitriev V G, Gurzadyan G G, Nikogosyan D N. Handbook of nonlinear optical crystals[M]. Springer, 2013.
[7] https://max.book118.com/html//2018/0329/159256906.shtm

Frank
Frank graduated from the University of Shanghai for Science and Technology, majoring in optics. As a technical engineer at Crylink Company, he deeply understands crystal materials and laser components.
Related Video(s) with this Article
Related Product(s) with this Article
Related Application(s) with this Article


